... newer stories
Freitag, 26. Februar 2016
Eine >5< ist keine >fünf< - Das Problem von Synästhesie und Mathe
nacy_marynow, 23:32h
Aufmerksamen Lesern ist sicher nicht entgangen, dass ich die Zahlen in den vorangegangenen Artikeln ausschließlich als Ziffern geschrieben habe. Das hat einen ganz einfachen Grund: in Worten sind sie für mich etwas anderes.
Hier kommt jetzt das erwähnte Farbensehen ins Spiel. Fast jeder Synästhesist hat das. Recherchiert man Synästhesie, ist das farbige Sehen von Zahlen und Buchstaben meist das erste, was man in diesem Zusammenhang findet. Doch anders als bei den meisten, existieren diese Farben bei mir auch nur bei gedruckten Zahlen und Buchstaben. Der Text, den ich hier gerade schreibe, würde auf Papier einfach nur die Farbe des Füllers haben. Hier, am Laptop eingetippt, ist er kunterbunt. Jeder Buchstabe hat dabei seine feste Farbe, völlig egal, in welchem Wort er gerade steht:
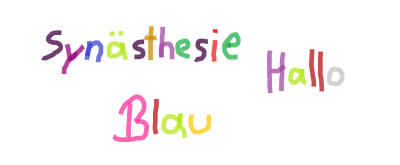
Hier wird es deutlich: Obwohl das Wort >blau< selbst eine Farbe beschreibt, kommt genau diese Farbe nicht einmal darin vor. Und dieses Phänomen ist, im abgewandelten Sinne, mein persönlicher Grund, warum ich noch nie gut in Mathe war - Mathe und meine Logik bezüglich Zahlen passen einfach nicht zusammen.
Natürlich hat auch jede Zahl ihre eigene Farbe:
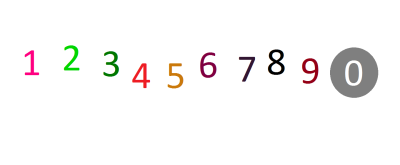
Diese Farben, im Gegensatz zu denender Buchstaben, stören mich. Das mag zum Einen daran liegen, dass Zahlen bei mir zusätzlich Empfindungen auslösen (was Buchstaben nicht tun); zum Anderen aber daran, dass ich mit den Zahlen rechnen muss.
Mathe war noch nie meine Stärke. Ich verstehe es einfach nicht. Die Erklärung dafür ist, aus meiner Sicht, ziemlich einfach, aber für Nicht-Synästhetiker ziemlich befremdlich.
Nehmen wir die einfache Rechnung
4 + 3 = 7
und gehen damit in meine Grundschulrechenzeit zurück. In meiner Wahrnehmung sähe die Rechung wie folgt aus, wobei schwarz hier für "keine Farbe" steht:
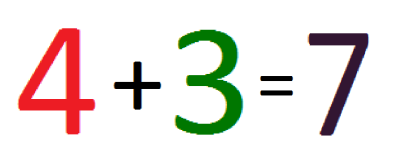
Das Ergebnis war für mich unlogisch, denn nimmt man den Farbkasten und mischt hellrot und dunkelgrün, kommt dabei kein reines Lila heraus. Wie also konnte es hier so sein? Und noch schwieriger:
9 + 9 = 18
also
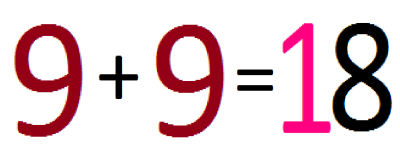
Wie kann zweimal dieselbe Farbe zu zwei verschiedenen Farben gleichzeitig werden? Ich habe es nie verstanden und ich werde es nie verstehen; und es ist vergebliche Mühe, zu versuchen, sich die Farbverläufe einzuprägen, denn bei so vielen Rechnungen auf der Welt würde mir der Kopf platzen.
Hier kommt jetzt das erwähnte Farbensehen ins Spiel. Fast jeder Synästhesist hat das. Recherchiert man Synästhesie, ist das farbige Sehen von Zahlen und Buchstaben meist das erste, was man in diesem Zusammenhang findet. Doch anders als bei den meisten, existieren diese Farben bei mir auch nur bei gedruckten Zahlen und Buchstaben. Der Text, den ich hier gerade schreibe, würde auf Papier einfach nur die Farbe des Füllers haben. Hier, am Laptop eingetippt, ist er kunterbunt. Jeder Buchstabe hat dabei seine feste Farbe, völlig egal, in welchem Wort er gerade steht:
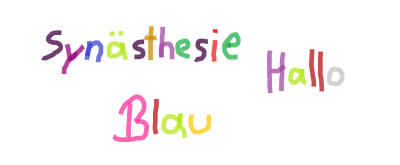
Hier wird es deutlich: Obwohl das Wort >blau< selbst eine Farbe beschreibt, kommt genau diese Farbe nicht einmal darin vor. Und dieses Phänomen ist, im abgewandelten Sinne, mein persönlicher Grund, warum ich noch nie gut in Mathe war - Mathe und meine Logik bezüglich Zahlen passen einfach nicht zusammen.
Natürlich hat auch jede Zahl ihre eigene Farbe:
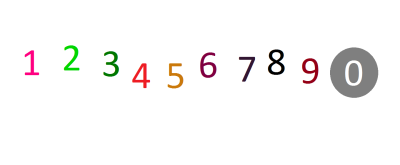
Diese Farben, im Gegensatz zu denender Buchstaben, stören mich. Das mag zum Einen daran liegen, dass Zahlen bei mir zusätzlich Empfindungen auslösen (was Buchstaben nicht tun); zum Anderen aber daran, dass ich mit den Zahlen rechnen muss.
Mathe war noch nie meine Stärke. Ich verstehe es einfach nicht. Die Erklärung dafür ist, aus meiner Sicht, ziemlich einfach, aber für Nicht-Synästhetiker ziemlich befremdlich.
Nehmen wir die einfache Rechnung
4 + 3 = 7
und gehen damit in meine Grundschulrechenzeit zurück. In meiner Wahrnehmung sähe die Rechung wie folgt aus, wobei schwarz hier für "keine Farbe" steht:
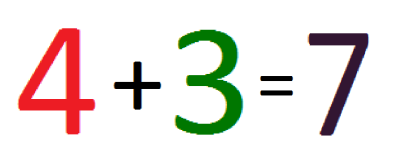
Das Ergebnis war für mich unlogisch, denn nimmt man den Farbkasten und mischt hellrot und dunkelgrün, kommt dabei kein reines Lila heraus. Wie also konnte es hier so sein? Und noch schwieriger:
9 + 9 = 18
also
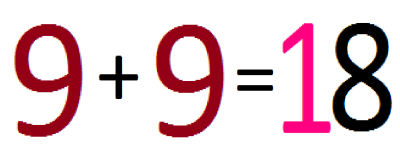
Wie kann zweimal dieselbe Farbe zu zwei verschiedenen Farben gleichzeitig werden? Ich habe es nie verstanden und ich werde es nie verstehen; und es ist vergebliche Mühe, zu versuchen, sich die Farbverläufe einzuprägen, denn bei so vielen Rechnungen auf der Welt würde mir der Kopf platzen.
... link (0 Kommentare) ... comment
Wie Synästhetiker Zahlen wahrnehmen
nacy_marynow, 22:47h
Aus der Geschichte mit meiner Mathelehrerin lernte ich zum ersten Mal, dass ich irgendwie anders wahrzunehmen schien als andere. Das heißt, damals dachte ich noch, die anderen nehmen anders wahr als ich! Die Sache mit der 9 beschäftigte mich noch jahrelang - Warum ist die 9 traurig?
Seit ich mir im Klaren darüber bin, was in meinem Kopf und meiner Wahrnehmung vor sich geht, weiß ich die Antwort darauf: Die 9 ist traurig, weil sie eine 9 ist; genau so, wie die 4 gehässig lacht, weil sie eine 4 ist. Das zu hinerfragen, ist genauso überflüssig wie die Frage, warum ein Habicht ein Habicht ist und kein Storch oder Wolf oder Zebra. Er ist eben ein Habicht, mit allem, was zu einem Habicht gehört - typisch gefärbte Federn, Klauen, gebogener Schnabel und große dunkle Augen. Das sind seine Merkmale, seine Eigenschaften, und wenn er diese nicht hätte, dann wäre er kein Habicht. Und das Merkmal der 9 ist eben, dass sie traurig ist. Zumindest ist das bei mir so. Und bei vielen Synästhetikern ist es ähnlich.

Die wohl bekannteste Form der Synästhesie sind farbige Zahlen und Buchstaben. Fast jeder, der Synästhesie besitzt, sieht diese Farben, ganz unabhängig davon, welche synästhetischen Wahrnehmungen er sonst noch besitzt. So wie auf dem Bild, so sehen unsere Zahlen aus. Was dabei ganz wichtig ist - Synästhesie ist individuell. Zwar hat jede Zahl ihre zugeordnete Farbe, doch diese Farbe ist bei jedem eine andere. Der eine sieht eine 1 rot, der nächste grün, wieder ein anderer orangegelb. Auch bei mir hat jede Zahl ihre eigene Farbe - dazu komme ich im nächsten Artikel noch einmal genauer. Ich habe aber noch eine weitere Wahrnehmung von Zahlen. Meine Form der Synästhesie ist, wie bereits erwähnt, die Gefühlssynästhesie. Ich verknüpfe also Dinge und Gefühle miteinander - um diesen Begriff jetzt einmal zu begrenzen.
Daher kommt die traurige 9, die ich als Kind so oft in meinem Mathebuch gesehen habe. Und so hat jede Zahl bei mir ihr ganz eigenes Merkmal.
- 1 ist eingebildet und hochnäsig
- 2 ist elegant und hübsch, jemand Edles
- 3 ist wild und ungebändigt
- 4 ist gehässig und hinterhältig, man sollte
ihr nicht vertrauen
- 5 weiß nicht, was sie will, ob rund oder
eckig, gut oder schlecht
- 6 hat eine Brille auf der Nase und ist eine
Besserwisserin
- 7 ist ganz der Akurate, der Ordnungstyp
- 8 ist pausenlos am Zweifeln und eiert in
Gedanken hin und her
- 9 ist traurig und einsam
- 0 ist schreckling ängstlich und schreckhaft
Bei mehrstelligen Zahlen, wie der 26, vermischen sich die Eigenschaften der einzelnen Zahlen. So ist die genannte 26 eine elegante Besserwisserin und eine 1379 eine hochnäsige Person, die sich nichts vorschreiben lässt, pingelig ist und heimlich vor sich hin weint.
Zudem gibt es weibliche Zahlen (1,2,3,6,9), männliche Zahlen (4,5,7,8) und eine sächliche Zahl (0). Anders als die Merkmale, welche ich ja nur bei gedruckten Zahlen empfinde (siehe "Frau Wagner, können Sie mir sagen, warum die 9 weint?"), gilt diese Geschlechtereinteilung in meinem Kopf auch bei handgeschriebenen Zahlen. Schließlich bleibt eine weibliche Person auch dann noch weiblich, wenn sie sich etwas anderes anzieht ;-)
Seit ich mir im Klaren darüber bin, was in meinem Kopf und meiner Wahrnehmung vor sich geht, weiß ich die Antwort darauf: Die 9 ist traurig, weil sie eine 9 ist; genau so, wie die 4 gehässig lacht, weil sie eine 4 ist. Das zu hinerfragen, ist genauso überflüssig wie die Frage, warum ein Habicht ein Habicht ist und kein Storch oder Wolf oder Zebra. Er ist eben ein Habicht, mit allem, was zu einem Habicht gehört - typisch gefärbte Federn, Klauen, gebogener Schnabel und große dunkle Augen. Das sind seine Merkmale, seine Eigenschaften, und wenn er diese nicht hätte, dann wäre er kein Habicht. Und das Merkmal der 9 ist eben, dass sie traurig ist. Zumindest ist das bei mir so. Und bei vielen Synästhetikern ist es ähnlich.

Die wohl bekannteste Form der Synästhesie sind farbige Zahlen und Buchstaben. Fast jeder, der Synästhesie besitzt, sieht diese Farben, ganz unabhängig davon, welche synästhetischen Wahrnehmungen er sonst noch besitzt. So wie auf dem Bild, so sehen unsere Zahlen aus. Was dabei ganz wichtig ist - Synästhesie ist individuell. Zwar hat jede Zahl ihre zugeordnete Farbe, doch diese Farbe ist bei jedem eine andere. Der eine sieht eine 1 rot, der nächste grün, wieder ein anderer orangegelb. Auch bei mir hat jede Zahl ihre eigene Farbe - dazu komme ich im nächsten Artikel noch einmal genauer. Ich habe aber noch eine weitere Wahrnehmung von Zahlen. Meine Form der Synästhesie ist, wie bereits erwähnt, die Gefühlssynästhesie. Ich verknüpfe also Dinge und Gefühle miteinander - um diesen Begriff jetzt einmal zu begrenzen.
Daher kommt die traurige 9, die ich als Kind so oft in meinem Mathebuch gesehen habe. Und so hat jede Zahl bei mir ihr ganz eigenes Merkmal.
- 1 ist eingebildet und hochnäsig
- 2 ist elegant und hübsch, jemand Edles
- 3 ist wild und ungebändigt
- 4 ist gehässig und hinterhältig, man sollte
ihr nicht vertrauen
- 5 weiß nicht, was sie will, ob rund oder
eckig, gut oder schlecht
- 6 hat eine Brille auf der Nase und ist eine
Besserwisserin
- 7 ist ganz der Akurate, der Ordnungstyp
- 8 ist pausenlos am Zweifeln und eiert in
Gedanken hin und her
- 9 ist traurig und einsam
- 0 ist schreckling ängstlich und schreckhaft
Bei mehrstelligen Zahlen, wie der 26, vermischen sich die Eigenschaften der einzelnen Zahlen. So ist die genannte 26 eine elegante Besserwisserin und eine 1379 eine hochnäsige Person, die sich nichts vorschreiben lässt, pingelig ist und heimlich vor sich hin weint.
Zudem gibt es weibliche Zahlen (1,2,3,6,9), männliche Zahlen (4,5,7,8) und eine sächliche Zahl (0). Anders als die Merkmale, welche ich ja nur bei gedruckten Zahlen empfinde (siehe "Frau Wagner, können Sie mir sagen, warum die 9 weint?"), gilt diese Geschlechtereinteilung in meinem Kopf auch bei handgeschriebenen Zahlen. Schließlich bleibt eine weibliche Person auch dann noch weiblich, wenn sie sich etwas anderes anzieht ;-)
... link (0 Kommentare) ... comment
... older stories