Freitag, 26. Februar 2016
Eine >5< ist keine >fünf< - Das Problem von Synästhesie und Mathe
nacy_marynow, 23:32h
Aufmerksamen Lesern ist sicher nicht entgangen, dass ich die Zahlen in den vorangegangenen Artikeln ausschließlich als Ziffern geschrieben habe. Das hat einen ganz einfachen Grund: in Worten sind sie für mich etwas anderes.
Hier kommt jetzt das erwähnte Farbensehen ins Spiel. Fast jeder Synästhesist hat das. Recherchiert man Synästhesie, ist das farbige Sehen von Zahlen und Buchstaben meist das erste, was man in diesem Zusammenhang findet. Doch anders als bei den meisten, existieren diese Farben bei mir auch nur bei gedruckten Zahlen und Buchstaben. Der Text, den ich hier gerade schreibe, würde auf Papier einfach nur die Farbe des Füllers haben. Hier, am Laptop eingetippt, ist er kunterbunt. Jeder Buchstabe hat dabei seine feste Farbe, völlig egal, in welchem Wort er gerade steht:
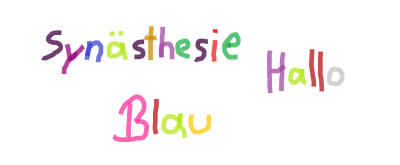
Hier wird es deutlich: Obwohl das Wort >blau< selbst eine Farbe beschreibt, kommt genau diese Farbe nicht einmal darin vor. Und dieses Phänomen ist, im abgewandelten Sinne, mein persönlicher Grund, warum ich noch nie gut in Mathe war - Mathe und meine Logik bezüglich Zahlen passen einfach nicht zusammen.
Natürlich hat auch jede Zahl ihre eigene Farbe:
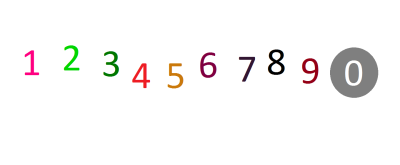
Diese Farben, im Gegensatz zu denender Buchstaben, stören mich. Das mag zum Einen daran liegen, dass Zahlen bei mir zusätzlich Empfindungen auslösen (was Buchstaben nicht tun); zum Anderen aber daran, dass ich mit den Zahlen rechnen muss.
Mathe war noch nie meine Stärke. Ich verstehe es einfach nicht. Die Erklärung dafür ist, aus meiner Sicht, ziemlich einfach, aber für Nicht-Synästhetiker ziemlich befremdlich.
Nehmen wir die einfache Rechnung
4 + 3 = 7
und gehen damit in meine Grundschulrechenzeit zurück. In meiner Wahrnehmung sähe die Rechung wie folgt aus, wobei schwarz hier für "keine Farbe" steht:
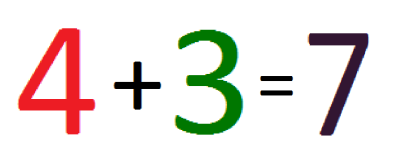
Das Ergebnis war für mich unlogisch, denn nimmt man den Farbkasten und mischt hellrot und dunkelgrün, kommt dabei kein reines Lila heraus. Wie also konnte es hier so sein? Und noch schwieriger:
9 + 9 = 18
also
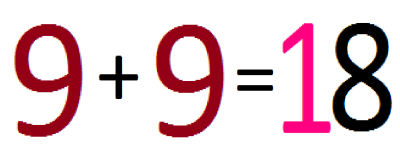
Wie kann zweimal dieselbe Farbe zu zwei verschiedenen Farben gleichzeitig werden? Ich habe es nie verstanden und ich werde es nie verstehen; und es ist vergebliche Mühe, zu versuchen, sich die Farbverläufe einzuprägen, denn bei so vielen Rechnungen auf der Welt würde mir der Kopf platzen.
Hier kommt jetzt das erwähnte Farbensehen ins Spiel. Fast jeder Synästhesist hat das. Recherchiert man Synästhesie, ist das farbige Sehen von Zahlen und Buchstaben meist das erste, was man in diesem Zusammenhang findet. Doch anders als bei den meisten, existieren diese Farben bei mir auch nur bei gedruckten Zahlen und Buchstaben. Der Text, den ich hier gerade schreibe, würde auf Papier einfach nur die Farbe des Füllers haben. Hier, am Laptop eingetippt, ist er kunterbunt. Jeder Buchstabe hat dabei seine feste Farbe, völlig egal, in welchem Wort er gerade steht:
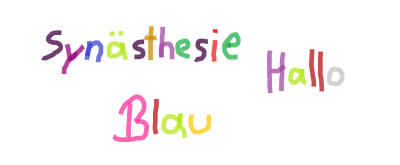
Hier wird es deutlich: Obwohl das Wort >blau< selbst eine Farbe beschreibt, kommt genau diese Farbe nicht einmal darin vor. Und dieses Phänomen ist, im abgewandelten Sinne, mein persönlicher Grund, warum ich noch nie gut in Mathe war - Mathe und meine Logik bezüglich Zahlen passen einfach nicht zusammen.
Natürlich hat auch jede Zahl ihre eigene Farbe:
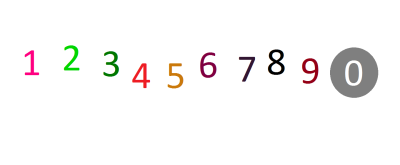
Diese Farben, im Gegensatz zu denender Buchstaben, stören mich. Das mag zum Einen daran liegen, dass Zahlen bei mir zusätzlich Empfindungen auslösen (was Buchstaben nicht tun); zum Anderen aber daran, dass ich mit den Zahlen rechnen muss.
Mathe war noch nie meine Stärke. Ich verstehe es einfach nicht. Die Erklärung dafür ist, aus meiner Sicht, ziemlich einfach, aber für Nicht-Synästhetiker ziemlich befremdlich.
Nehmen wir die einfache Rechnung
4 + 3 = 7
und gehen damit in meine Grundschulrechenzeit zurück. In meiner Wahrnehmung sähe die Rechung wie folgt aus, wobei schwarz hier für "keine Farbe" steht:
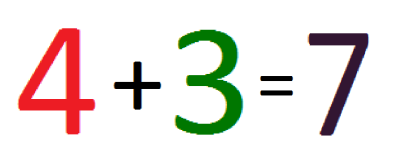
Das Ergebnis war für mich unlogisch, denn nimmt man den Farbkasten und mischt hellrot und dunkelgrün, kommt dabei kein reines Lila heraus. Wie also konnte es hier so sein? Und noch schwieriger:
9 + 9 = 18
also
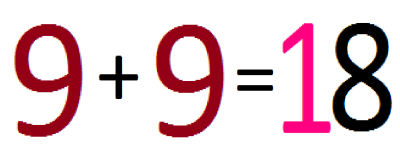
Wie kann zweimal dieselbe Farbe zu zwei verschiedenen Farben gleichzeitig werden? Ich habe es nie verstanden und ich werde es nie verstehen; und es ist vergebliche Mühe, zu versuchen, sich die Farbverläufe einzuprägen, denn bei so vielen Rechnungen auf der Welt würde mir der Kopf platzen.
... comment